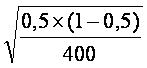[Материалы для студентов-историков]
Информатика и математика - материалы для экзамена
Выборочный метод
Основные понятия
• Множество всех единиц статистической совокупности носит название генеральной совокупности . Многие задачи статистического анализа связаны с описанием больших совокупностей объектов.
• Зачастую на практике по тем или иным причинам невозможно рассмотреть все элементы таких совокупностей. В этом случае ограничиваются изучением лишь некоторой части генеральной совокупности. Эта часть называется выборочной совокупностью или выборкой .
• Полученные при изучении выборки результаты стремятся распространить на всю генеральную совокупность.
• Для этого выборка должна быть не любой произвольной частью генеральной совокупности, а такой ее частью, которая достаточно правильно отражает основные параметры этой совокупности.
• Таким образом, выборка должна быть репрезентативной (представи - тельной).
• Каким образом можно добиться репрезентативности выборки, т.е. того, чтобы она правильно отражала основные свойства, присущие генеральной совокупности?
• Ответ кажется, на первый взгляд, довольно парадоксальным: выборка должна быть случайной . Что это значит?
• Случайность никоим образом не отождествляется со стихийностью или произвольностью отбора – напротив, случайность означает то, что все объекты генеральной совокупности должны иметь равные шансы попасть в выборку .
• Наиболее простым является случайный отбор, например, при помощи обычной жеребьевки .
• Для случайного отбора часто используются т.н. таблицы случайных чисел.
• Для более обширных, но достаточно однородных совокупностей используется механический отбор (применявшийся еще в земской статистике).
• Для неоднородных совокупностей с определенной структурой чаще применяется типический отбор .
• Существуют и другие методы, в том числе – комбинации разных способов отбора на нескольких этапах построения выборочной совокупности.
* * *
• Однако никакая, даже самым тщательным образом сформированная выборка, не может дать точного знания о генеральной совокупности.
• Таким образом, в выборочных результатах всегда присутствуют ошибки . Эти ошибки можно разделить на два класса:
• случайные,
• систематические.
• К случайным ошибкам относятся отклонения выборочных характеристик от генеральных (например, отклонения среднего значения признака в выборке от среднего значения этого признака в генеральной совокупности.
• Случайные ошибки обусловлены самой природой выборочного метода, и поэтому они неизбежны .
• Однако величина случайной ошибки поддается вычислению (оценке).
• Систематические ошибки, наоборот, не носят случайного характера; они связаны с отклонением структуры выборки от реальной структуры генеральной совокупности.
• Систематические ошибки появляются тогда, когда нарушается основное правило случайного отбора – обеспечение для всех объектов равных шансов попасть в выборку.
• Необходимо строить выборку так, чтобы устранить систематические ошибки.
• Основными источниками систематических ошибок являются:
• неадекватность сформированной выборки задачам исследования;
• незнание характера распределения в генеральной совокупности и, как следствие, нарушение в выборке структуры генеральной совокупности;
• сознательный отбор наиболее удобных и выигрышных элементов генеральной совокупности.
Выборочный метод
Статистическое оценивание среднего значения количественного признака
Теория статистического оценивания
• Идея статистического оценивания параметров генеральной совокупности по выборочным данным сводится к тому, что выборочная характеристика какого-либо параметра (например, среднего арифметического значения признака) является не точным, а приближенным значением – оценкой – этого же параметра в генеральной совокупности (как правило, значение в генеральной совокупности неизвестно.
Теория статистического оценивания
• Возникает вопрос: как сильно отклоняется эта оценка от истинного значения? В частности, нельзя ли указать такую величину ошибки , которая "практически достоверно" (т.е. с вероятностью, близкой к единице) гарантировала бы, что выборочная оценка не отличается от неизвестного значения более чем на величину этой ошибки?
Теория статистического оценивания
• То есть, нельзя ли указать вокруг выборочного значения такой интервал, который бы с заданной (достаточно высокой) вероятностью – доверительной вероятностью – "накрывал" бы истинное значение этого параметра?
• Этот интервал в математической статистике называется доверительным интервалом ; его величина зависит как от доверительной вероятности (т.е. надежности оценивания), так и от объема выборки.
Ошибка среднего
• В качестве примера рассмотрим данные промышленной переписи 1900 г. по предприятиям Закавказья (файл Industry.sta) как генеральную совокупность (1060 предприятий).
• Среднее число рабочих на предприятии равно 77 чел. (по всей генеральной совокупности).
Ошибка среднего
• Случайный отбор 5% объектов (53 предприятия) дает среднее число рабочих, равное 81 чел. Ошибка выборки, очевидно связанная с тем, что не все 1060 предприятий попали в выборку, равна разности между этими средними – генеральным средним ( 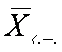 ) и выборочным (
) и выборочным ( 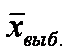 ).
).
Ошибка среднего
• Если сформировать другую выборку того же объема из нашей генеральной совокупности, она даст другую величину ошибки и т.д.
• Оказывается, что все эти выборочные средние при достаточно больших выборках распределены нормально вокруг генеральной средней при достаточно большом числе повторений выборки одного и того числа объектов из генеральной совокупности.
Ошибка среднего
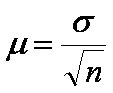
• При этом неизбежный разброс выборочных средних вокруг генеральной средней (т.е. стандартное отклонение выборочных средних) называется стандартной ошибкой выборки m , которая выражается формулой:
где s – среднее квадратическое отклонение, n – объем выборки.
Ошибка среднего
• Стандартная ошибка среднего значения ( Standard Error of Mean ) измеряется в тех же единицах, что и среднее квадратическое отклонение признака.
• Стандартная ошибка выборки тем меньше, чем меньше величина s (которая характеризует разброс значений признака) и чем больше объем выборки n .
Ошибка среднего
• В нашем примере величина s в генеральной совокупности известна точно и равна 187 чел.; по формуле для ошибки выборки легко подсчитать, что m » 26 чел.
• Это значит, что с определенной долей уверенности можно говорить, что большинство выборочных средних должно находиться в интервале 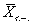 ± m . Например, для нашей выборки число 81 попало в интервал 77 ± 26 (в интервал от 52 до 103).
± m . Например, для нашей выборки число 81 попало в интервал 77 ± 26 (в интервал от 52 до 103).
Ошибка среднего
• Что значит "большинство" выборочных средних?
• Для нормального распределения (а распределение выборочных средних как раз и является нормальным) известно, какая часть совокупности попадает в любой интервал вокруг среднего значения. В частности:
• 67% всех выборочных средних попадут в интервал ± m ;
• 95% – в интервал 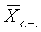 ± 2 m ;
± 2 m ;
• 99,7% – в интервал 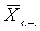 ± 3 m .
± 3 m .
Ошибка среднего
• На практике проблема заключается, однако, в том, что характеристики генеральной совокупности нам не известны, а выборка делается именно с целью их оценки.
Ошибка среднего
• 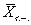 Поэтому вместо величины известна для выборки, и s тоже считается по выборке. Значит, если мы будем делать выборки одного и того же объема n из генеральной совокупности, то в 67% случаев на интервале
Поэтому вместо величины известна для выборки, и s тоже считается по выборке. Значит, если мы будем делать выборки одного и того же объема n из генеральной совокупности, то в 67% случаев на интервале 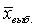 ± m будет находиться значение
± m будет находиться значение 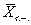 (оно же в 95% случаев будет находится на интервале
(оно же в 95% случаев будет находится на интервале 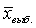 ± 2 m и в 99,7% случаев – на интервале
± 2 m и в 99,7% случаев – на интервале 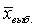 ± 3 m ).
± 3 m ).
Ошибка среднего
• Поскольку реально делается только одна выборка, то формулируется это утверждение в терминах вероятности: с вероятностью 67% среднее значение признака в генеральной совокупности заключено в интервале 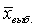 ± m (с вероятностью 95% – в интервале
± m (с вероятностью 95% – в интервале 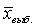 ± 2 m и т.д.).
± 2 m и т.д.).
Теория статистического оценивания
• На практике вокруг выборочного значения строится такой интервал, который бы с заданной (достаточно высокой) вероятностью – доверительной вероятностью – "накрывал" бы истинное значение этого параметра в генеральной совокупности.
• Этот интервал в математической статистике называется доверительным интервалом .
Теория статистического оценивания
• Доверительная вероятность P – это степень уверенности в том, что доверительный интервал действительно будет содержать истинное (неизвестное) значение параметра в генеральной совокупности.
• Доверительная вероятность выражается процентом выборок данного объема, которые дают доверительные интервалы, содержащие значение в генеральной совокупности.
Теория статистического оценивания
• Например, если доверительная вероятность P равна 0,90 или 90%, это значит, что 90 выборок из 100 (то есть 0,90 или 90%) дадут правильную оценку параметра в генеральной совокупности.
• Соответственно, вероятность ошибки, т.е. неверной оценки генерального среднего по выборке, равна 1 – P ( в процентах – 100% - P ). Для данного примера это значит, что 10 выборок из 100 (0,1 или 10% дадут неверную оценку.
Теория статистического оценивания
• Очевидно, что степень уверенности (доверительная вероятность) зависит от величины интервала: чем шире интервал, тем выше уверенность , что в него попадет неизвестное значение для генеральной совокупности.
• На практике для построения доверительного интервала берется, как минимум, удвоенная ошибка выборки, чтобы обеспечить уверенность не менее 95%.
Доверительный интервал для среднего
• Величина доверительного интервала
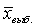 ± t m пропорциональна ошибке выборки μ .
± t m пропорциональна ошибке выборки μ .
• Кроме того, величина доверительного интервала зависит от параметра t , который выбирается, исходя из требуемого уровня надежности.
• Значение параметра t = 1 соответствует уверенности 67%, t = 2 – уверенности 95%, а t = 3 – уверенности 99,7%.
Доверительный интервал для среднего
• Величина D = t m , которая в целом определяет величину доверительного интервала, называется предельной ошибкой выборки или точностью оценки
• Параметр t показывает во сколько раз предельная ошибка D превышает среднюю ошибку выборки m .
Доверительный интервал для среднего
• Пример . Ниже показаны границы доверительного интервала для среднего значения числа рабочих в генеральной совокупности по выборке из 53 предприятий при степени уверенности 95%.
• Получен доверительный интервал [32, 131] (при этом известное нам значение 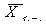 , равное 77 чел., действительно находится на этом интервале).
, равное 77 чел., действительно находится на этом интервале).

Доверительный интервал для среднего
• Точность ( Δ ) и уверенность (надежность) ( P ) оценки находятся в обратной зависимости: чем больше точность (т.е. чем меньше предельная ошибка и уже доверительный интервал), тем меньше надежность такой оценки (степень уверенности).
• И наоборот – чем ниже точность оценки, тем выше ее надежность .
Доверительный интервал для среднего
Точность увеличивается |
Точность уменьшается |
Предельная ошибка D уменьшается |
Предельная ошибка D увеличивается |
Доверительный интервал суживается |
Доверительный интервал расширяется |
Уверенность (надежность) уменьшается |
Уверенность (надежность) увеличивается |
Доверительный интервал для среднего
• Последовательность действий при построении доверительного интервала:
• По выборке вычисляется 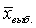 и σ .
и σ .
• Вычисляется средняя ошибка выборки μ .
• Выбирается доверительная вероятность P и соответствующее ей значение параметра t .
• Вычисляется предельная ошибка Δ как произведение t и μ .
• Строится интервал 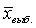 ± t m .
± t m .
Выборочный метод
Определение объема выборки для оценки среднего значения количественного признака
Определение объема выборки
• Исследователь всегда ставит перед собой задачу создания выборки, которая давала бы оценку параметров генеральной совокупности с определенной точностью D и надежностью (уверенностью) P.
• Таким образом, формирование выборочной совокупности начинается с определения того, какое количество объектов надо включить в выборку, чтобы она обеспечивала искомые точность и надежность.
Определение объема выборки
• В соответствии с формулой для ошибки выборки количество объектов (или объем выборки) n определяется по формуле:
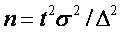 ,
,
где параметр t определяется по специальным таблицам нормального распределения в зависимости от величины надежности P (в частности, для надежности 95% t равно 2),
s – среднее квадратическое отклонение признака в генеральной совокупности (или в выборке).
Определение объема выборки
• Одна из проблем выборочного метода состоит в том, что пока выборка не сделана, величина s в формуле для объема выборки не известна, поэтому для окончательного формирования выборки приходится делать предварительную или пробную выборку для определения s .
Определение объема выборки
• Пример . Определить, сколько предприятий Закавказья следует отобрать, чтобы определить среднее число рабочих на предприятии с надежностью 95% и точностью 20 чел. (в качестве s взять величину 187 чел.).
• Поскольку степень надежности P = 95%, в качестве значения t выбираем 2.
• Подставив в формулу для n все необходимые значения, получим: (2) 2 (187) 2 / (20) 2 = 350.
• Таким образом, надо отобрать для изучения 350 предприятий.
Выборочный метод
Статистическое оценивание доли качественного признака
Ошибка доли
• Если выборочный метод используется для работы с неколичественными данными, то роль среднего арифметического значения в совокупности играет доля или частота признака.
• Доля (обозначается q ) вычисляется как отношение числа объектов, обладающих данным признаком ( n 0 ), к числу объектов во всей совокупности: q = n 0 / n .
• Доля часто выражается в процентах.
Ошибка доли
• Роль меры рассеяния качественного признака играет величина
• Стандарная ошибка выборки m для оценки доли качественного признака в генеральной совокупности вычисляется по формуле:
• Стандартная ошибка доли качественного признака также часто выражается в %.
Ошибка доли
• Пример . Найдем, пользуясь этой формулой, стандартную ошибку 5% выборки из генеральной совокупности промышленных предприятий Закавказья (53 предприятия из общего числа 1060) при определении доли частных предприятий.
• По данным выборки из 53 предприятий оказалось 38 частных, т.е. доля частных равна 0,72 (или 72%).
• Стандартная ошибка выборки объема 53 по приведенной формуле равна » 0,06 (или 6%).
Доверительный интервал для доли
• Используя стандарную ошибку выборки, можно построить доверительный интервал для доли: 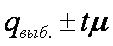
• Для этого надо взять значение t , которое связано с уровнем надежности P . Если P равно 95%, то, как известно, t = 2.
• Значит, с вероятностью 95% можно утверждать, что неизвестное значение доли частных предприятий в генеральной совокупности лежит в границах
0,72 ± 2(0,06), т.е. от 0,60 до 0,84 (или от 60 до 84%).
Доверительный интервал для доли
• Последовательность действий при построении доверительного интервала:
• По выборке вычисляется  .
.
• Вычисляется средняя ошибка выборки μ .
• Выбирается доверительная вероятность P и соответствующее ей значение параметра t .
• Вычисляется предельная ошибка Δ как произведение t и μ .
• Строится интервал 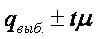
Выборочный метод
Определение объема выборки для оценки доли качественного признака
Определение объема выборки
• Пользуясь формулой для стандартной ошибки выборки для качественного признака, можно получить и формулу объема выборки для определения неизвестного значения доли качественного признака в генеральной совокупности с заданными точностью D и надежностью P . Эта формула имеет вид:
Определение объема выборки
• Определим объем выборки, которая с надежностью 95% должна оценить долю частных предприятий, и точность оценки ( D ) должна быть равной 0,05 (5%).
• Пользуясь приведенной выше формулой для n , получим
n = (2) 2 (0,72)(1–0,72)/(0,05) 2 » 161, т.е. 161 предприятие.
Сравнение выборочных средних
Сравнение выборочных средних
• С помощью доверительных интервалов можно сравнивать средние значения какого-либо признака для разных выборок.
• Если выборочные средние достаточно близки, это свидетельствует о том, что соответствующие генеральные совокупности не различаются по данному признаку, а реальные расхождения в значениях средних объясняются просто случайностями выборок, являются статистически незначимыми .
Сравнение выборочных средних
• Если же выборочные средние заметно различаются, это, скорее всего, связано с тем, что и соответствующие этим выборкам генеральные совокупности различаются по данному признаку, т.е. наблюдаемые различия статистически значимы .
• Как правило, в статистике проверяется гипотеза о том, что наблюдаемые различия выборочных средних являются статистически незначимыми.
Сравнение выборочных средних
• Какие же различия между выборочными средними являются достаточно малыми или достаточно большими?
• Представление о том, каковы возможные средние значения в соответствующих генеральных совокупностях, дают доверительные интервалы, построенные для обоих выборочных средних.
• Величина интервалов зависит от выбранного уровня доверительной вероятности P (например, 95%).
Сравнение выборочных средних
• Если построенные доверительные интервалы не пересекаются , это значит, что с высокой степенью вероятности средние значения в генеральных совокупностях различны.
• В этом случае гипотеза о том, что эти средние одинаковы, отклоняется, а различие между выборочными средними считается статистически значимым (т.е. существенным).
Сравнение выборочных средних
• Если же доверительные интервалы пересекаются , это значит, что с высокой степенью вероятности средние значения в генеральных совокупностях одинаковы.
• В этом случае гипотеза о совпадении средних в генеральных совокупностях не отклоняется, а различие между выборочными средними считается статистически незначимым (несущественным).
Сравнение выборочных средних
• Пример . В файле General.sta хранятся некоторые биографические данные о лицах, входивших в высший командный состав Советской армии в период Второй мировой войны. Среди переменных есть "год вступления в армию" и "год вступления в партию".
• Средние значения этих признаков равны, соответственно, 1918,9 и 1924,9.
• Является ли различие между ними статистически значимым?
Сравнение выборочных средних
• Доверительный интервал для среднего значения признака "год вступления в армию" для уровня значимости 95% равен [1918,7; 1919,2].
• Доверительный интервал для среднего значения признака "год вступления в партию" для уровня значимости 95% равен [1923,9; 1925,8].
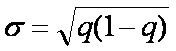
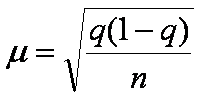
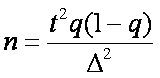

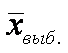 и σ ;
и σ ; 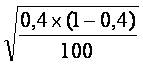 ; μ 2 =
; μ 2 =