ISKUNSTvo
[Материалы для студентов-историков]
Информатика и математика - материалы для экзамена
КОРРЕЛЯЦИОННЫЙ
И РЕГРЕССИОННЫЙ АНАЛИЗ
АНАЛИЗ ПАРНЫХ ВЗАИМОСВЯЗЕЙ
Основные понятия
• Связь как синхронность (согласованность) – корреляционный анализ.
• Связь как зависимость (влияние) – регрессионный анализ (причинно-следственные связи).
Основные понятия
• В регрессионном анализе один из признаков зависит от другого.
• Первый (зависимый) признак называется в регрессионном анализе результирующим , второй (независимый) – факторным .
• Не всегда можно однозначно определить, какой из признаков является независимым, а какой – зависимым. Часто связь может рассматриваться как двунаправленная.
Этапы анализа
• Выявление наличия взаимосвязи между признаками;
• Определение формы связи;
• Определение силы (тесноты) и направления связи.
Выявление наличия связи между признаками
Диаграммы рассеяния
Диаграмма рассеяния ( scatterplot )
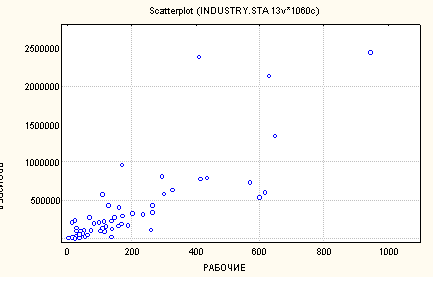
Определение формы связи
Линейная связь
Форма связи
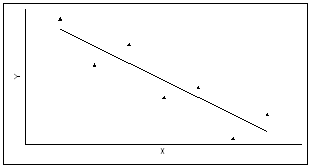
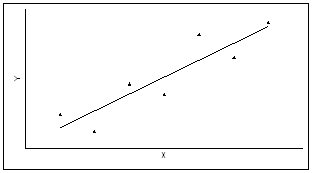
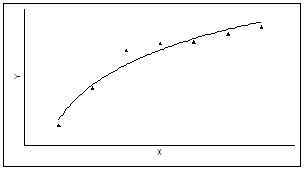
• Поскольку наиболее простой формой зависимости в математике является прямая, то в корреляционном и регрессионном анализе наиболее популярны линейные модели .
• Однако иногда расположение точек на диаграмме рассеяния показывает нелинейную зависимость либо вообще отсутствие связи между признаками.
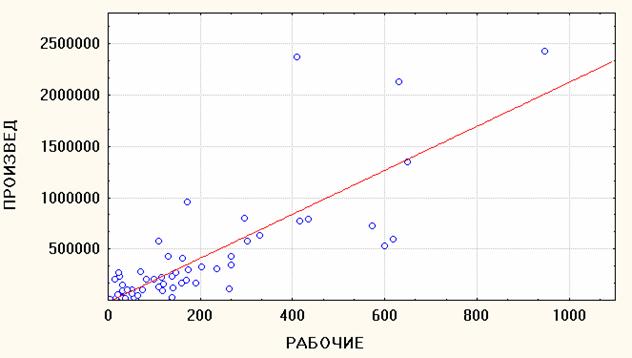
Линия регрессии и уравнение регрессии
Диаграмма рассеяния
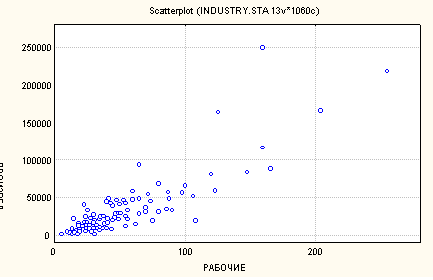
Линия регрессии
Линия регрессии
• Вычисляемая с помощью метода наименьших квадратов прямая линия называется линией регрессии . Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями).
• Линия регрессии дает наилучшее приближенное описание линейной зависимости между двумя переменными.
Уравнение парной линейной регрессии
• Как известно, прямая линия описывается уравнением вида:
Y = kX + b
где Y – результирующий признак, X – факторный признак, k и b – числовые параметры уравнения.
• Коэффициент k в уравнении регрессии называется коэффициентом регрессии .
Смысл коэффициента регрессии
• В общем случае коэффициент регрессии k показывает, как в среднем изменится результативный признак ( Y ), если факторный признак ( X ) увеличится на единицу .
Пример уравнения регрессии
• На диаграмме рассеяния показаны не только точки-объекты и теоретическая линия регрессии, но и уравнение этой (прямой) линии:
Y = 8 . 761 e 4 + 2. 984 e 3 * X
• Это уравнение записано в необычной форме, которая читается следующим образом:
Y = 87610 + 2984 X
Пример интерпретации коэффициента регресии
• В уравнении Y = 87610 + 2984 X
коэффициент регрессии равен +2984. Что это означает?
• В данном случае смысл коэффициента регрессии состоит в том, что увеличение числа рабочих на 1 чел. приводит в среднем к увеличению объема годового производства на 2984 руб.
Свойства коэффициента регрессии
• Коэффициент регрессии принимает любые значения.
• Коэффициент регрессии не симметричен , т.е. изменяется, если X и Y поменять местами.
• Единицей измерения коэффициента регрессии является отношение единицы измерения Y к единице измерения X
([ Y ] / [ X ]).
• Коэффициент регрессии изменяется при изменении единиц измерения X и Y .
Пример единицы измерения коэффициента регрессии
• В уравнении Y = 87610 + 2984 X
коэффициент регрессии равен 2984. В каких единицах он измеряется?
• Поскольку результативный признак Y измеряется в рублях, а факторный признак X в количестве рабочих (чел.), то коэффициент регрессии измеряется в рублях на человека (руб. / чел.)
Сравнение коэффициентов корреляции и регрессии
Коэффициент корреляции
• Принимает значения в диапазоне от -1 до +1
• Безразмерная величина
• Показывает силу связи между признаками
• Знак коэффициента говорит о направлении связи
Коэффициент регрессии
• Может принимать любые значения
• Привязан к единицам измерения обоих признаков
• Показывает структуру связи между признаками
• Знак коэффициента говорит о направлении связи
МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
Усложнение модели
• Обычно на зависимую переменную действуют сразу несколько факторов, среди которых трудно выделить единственный или главный.
• При этом факторы, влияющие на зависимую переменную, как правило, не являются независимыми друг от друга.
Пример
• Уравнение парной регрессии для зависимости объема производства ( Y ) от числа рабочих ( X 1 ) имеет вид:
Y = 87610 +2984 X 1
• Если построить уравнение парной регрессии для зависимости объема производства ( Y ) от мощности двигателей ( X 2 ), получим:
Y = 265300 +299,7 X 2
Пример
• Итак доход предприятия зависит одновременно от двух факторов производства – числа рабочих и энерговооруженности, однако эти факторы сами не являются независимыми друг от друга.
• Поэтому совокупная зависимость дохода от рабочих и мощности двигателей не есть простая сумма двух парных зависимостей.
Пример
• Следовательно, неверно , что суммарное влияние обоих факторов можно записать в виде суммы двух предыдущих уравнений:
Y = 3529 10 + 2 984 X 1 + 299,7 X 2
Пример
• Нельзя суммировать влияние нескольких факторов и на уровне корреляции.
• Так, коэффициент парной корреляции между суммой производства и числом рабочих равен 0,52, а между суммой производства и мощностью двигателей равен 0,3.
• Однако это не означает , что оба фактора дают суммарный коэффициент корреляции, равный 0,82.
Пример
• Наконец, если коэффициент детерминации между суммой производства и числом рабочих равен 27%, а между суммой производства и мощностью двигателей равен 9%, это
не означает , что оба фактора в сумме определяют сумму производства на 36%.
Мультиколлинеарность
• Невозможность сложения влияний отдельных факторов связана с эффектом мультиколлинеарности, или влиянием независимых факторов друг на друга.
• При этом каждый фактор влияет на результат как непосредственно, так и опосредованно, через связь с другими факторами.
Усложнение модели
• Таким образом, совокупное влияние всех независимых факторов на зависимую переменную не может быть представлено как простая сумма нескольких парных регрессий.
• Это совокупное влияние находится более сложным методом - методом множественной регрессии .
Модель множественной регрессии
Визуализация множественной связи
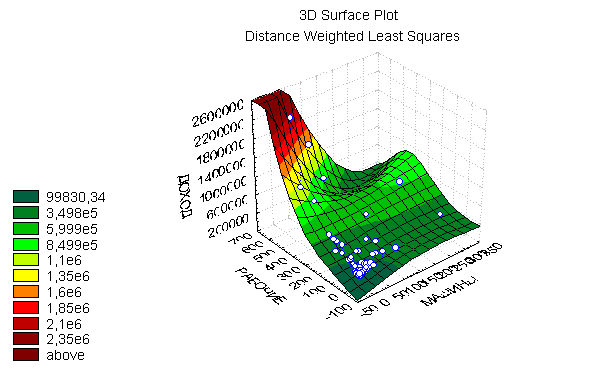
Уравнение множественной линейной регрессии
Y = a + b 1 X 1 + b 2 X 2 +…+ b k X k
X 1 , X 2 , … , X k независимые переменные (факторы);
b 1 , b 2 , … , b k соответствующие им коэффициенты регрессии
Коэффициенты регрессии
• Смысл коэффициента регрессии в уравнении множественной регрессии состоит в том, что он показывает как в среднем изменится значение результативного признака , если соответствующий факторный признак увеличится на единицу при фиксированных значениях всех остальных факторов.
Влияние мультиколлинеарности
• При наличии существенной мультиколлинеарности приведенная интерпретация коэффициентов уравнения множественной регрессии становится невозможной, поэтому при построении регрессионных моделей влияние мультиколлинеарности следует минимизировать, например, из каждой группы тесно связанных факторных признаков оставлять только один.
Основные результаты множественной регрессии
• КОЭФФИЦИЕНТ МНОЖЕСТВЕННОЙ КОРРЕЛЯЦИИ R
• СООТВЕТСТВУЮЩИЙ КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ R 2
• ЗНАЧИМОСТЬ РЕГРЕССИОННОЙ МОДЕЛИ
• КОЭФФИЦИЕНТЫ РЕГРЕССИИ И УРОВНИ ИХ ЗНАЧИМОСТИ
• ЧАСТНЫЕ КОЭФФИЦИЕНТЫ КОРРЕЛЯЦИИ
Коэффициент множественной корреляции
• Коэффициент множественной корреляции R является обобщением коэффициента парной корреляции для случая, когда число независимых факторов, включенных в уравнение, больше одного.
• R является величиной безразмерной.
• R не меняется при изменении единиц измерения соответствующих признаков.
• R принимает значения в интервале [0;1].
Коэффициент детерминации R 2
• Чем больше R , тем сильнее линейная связь между совокупностью независимых факторов и результативным признаком.
• Как и в случае парной зависимости, интерпретируется не сам коэффициент корреляции, а его квадрат – коэффициент детерминации.
• Этот коэффициент является квадратом соответствующего коэффициента корреляции и выражается в процентах.
Смысл коэффициента детерминации R 2
• Коэффициент детерминации R 2 показывает, насколько изменения зависимого признака (в процентах) объясняются изменениями совокупности независимых признаков . То есть, это доля дисперсии зависимого признака, объясняемая влиянием независимых признаков.
Значимость регрессионной модели
• Если коэффициент множественной корреляции вычислен на основе выборочных данных, то возможно, что его значение не отражает реальной связи между признаками, а получено в данной выборке случайно (при этом в генеральной совокупности признаки независимы).
Значимость регрессионной модели
• В основе проверки значимости регрессии лежит идея разложения дисперсии (разброса) результативного признака на факторную и остаточную дисперсии, т.е. объясненную (за счет независимых факторов) часть дисперсии и часть, оставшуюся необъясненной в рамках данной модели.
Значимость регрессионной модели
• Мерой значимости регрессии служит значение т.н. F- критерия – отношения факторной дисперсии к остаточной .
• Чем лучше регрессионная модель, тем выше доля факторной и ниже доля остаточной дисперсии.
Значимость регрессионной модели
• Для каждого значения F можно вычислить соответствующую вероятность. Если значение этой вероятности меньше принятого уровня значимости p или вероятности ошибки (в программе Statistica это 5% или 0,05), гипотеза об отсутствии линейной связи между результативным и факторными признаками отклоняется и регрессия признается значимой .
Пример
• Построим уравнение множественной регрессии для зависимости объема произведенной продукции (результативный признак) от числа рабочих и мощности двигателей (факторные признаки).
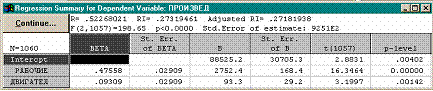
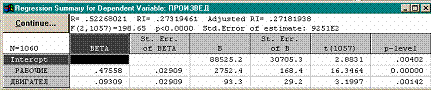
ОКНО РЕЗУЛЬТАТОВ
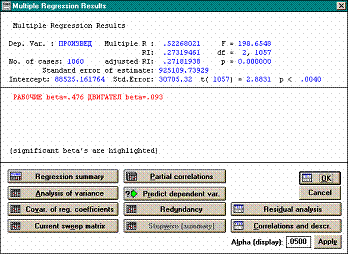
Пример
• Значение коэффициента множественной корреляции R равно 0,52.
• Соответствующий коэффициент детерминации R 2 равен 0,27, т.е. учтенные в модели факторные признаки объясняют результативные признак на 27%.
• Значение F -критерия равно 198, а соответствующий ему уровень значимости p практически равен нулю, т.е. заведомо меньше 0,05. Таким образом, данная модель статистически значима.
Пример
• Однако при общей значимости модели отдельные факторы могут играть разную роль, поэтому необходимо проверить и значимость каждого из факторов в отдельности в уравнении регрессии.
• Как увидеть построенное в программе Statistica уравнение множественной регрессии?
Уравнение множественной регрессии
• Столбец B содержит все параметры уравнения регрессии: два коэффициента регрессии и свободный член.
• Уравнение можно записать в виде:
Y = 88525 + 2752 X 1 + 93 X 2 ,
где X 1 – " рабочие " , X 2 – " двигатели " .
Коэффициенты регрессии и их интерпретация
• В полученном уравнении Y = 88525 + 2752 X 1 + 93 X 2 коэффициент регрессии 2752 означает, что увеличение числа рабочих на 1 чел. в среднем приводит к повышению объема производства на 2752 руб. при условии, что мощность двигателей не изменяется .
Коэффициенты регрессии и их интерпретация
• В уравнении Y = 88525 + 2752 X 1 + 93 X 2 коэффициент регрессии при втором факторе означает, что увеличение суммарной мощности двигателей на 1 л .с. приводит в среднем к увеличению объема производства на 93 руб. при условии, что число рабочих не изменяется .
Проверка значимости коэффициентов регрессии
• Проверка значимости коэффициентов регрессии означает проверку гипотезы об отсутствии связи между результативным и каждым из факторных признаков. Такая гипотеза означает, что ненулевые значения регрессионных коэффициентов обусловлены лишь случайностями выборки, а в генеральной совокупности все коэффициенты этого уравнения равны нулю.
Проверка значимости коэффициентов регрессии
• Для проверки значимости каждого коэффициента регрессии вычисляется t -статистика, которая показывает, во сколько раз этот коэффициент превышает свою среднюю ошибку в выборке.
• Соответствующая величина p (уровень значимости или вероятность ошибки) измеряет вероятность случайного появления в выборке значений t , равных или больших, чем данное значение.
Проверка значимости коэффициентов регрессии
• Если вероятность p меньше выбранного уровня значимости (по умолчанию 5% или 0,05), соответствующий коэффициент регрессии является статистически значимым .
• Если вероятность p больше выбранного уровня значимости , соответствующий коэффициент регрессии является статистически незначимым .
Проверка значимости коэффициентов регрессии
• Чем больше по абсолютной величине значение t , тем меньше соответствующая вероятность p .
• Например, величина t для коэффициентов, значимых на уровне 5%, больше 2 по модулю .
Проверка значимости коэффициентов регрессии
• Проверка значимости коэффициентов регрессии важна потому, что коэффициенты регрессии, в отличие от коэффициентов корреляции, не имеют максимальных и минимальных значений и их величины зависят от единиц измерения соответствующих признаков.
• Значит, сама по себе величина коэффициента регрессии никак не определяет силу влияния фактора на результат.
Проверка значимости коэффициентов регрессии
• Например, существенным в модели может оказаться и небольшой коэффициент регрессии, если этот коэффициент значимый.
• Если же коэффициент незначимый, то независимо от его величины следует считать, что соответствующий фактор не оказывает реального влияния на результативный признак.
Использование регрессионного анализа
• ПОСТРОЕНИЕ МОДЕЛЕЙ , объясняющих механизм влияния факторных признаков на результат.
• СТАТИСТИЧЕСКИЙ ПРОГНОЗ - вычисление значения результативной переменной для любых значений факторов.
• ВОСПОЛНЕНИЕ ПРОПУСКОВ в данных.
