[Материалы для студентов-историков]
Информатика и математика - материалы для экзамена
Факторный анализ
• Изучение зависимостей между признаками, описывающими сложное явление или процесс, неизменно ставит вопрос: каковы причины, обусловившие именно данную структуру связей? Сложные зависимости такой системы признаков весьма трудно "распутать", тем более что взаимосвязи признаков (измеряемые, например, коэффициентами корреляции) могут интерпретироваться не только как зависимости одних признаков от других, но и как зависимости от неких скрытых параметров, определяющих изменение целых групп коррелированных признаков.
Факторный анализ
• Общая причина изменений взаимосвязанных признаков ведет к тому, что в силу своей согласованности они в некотором смысле дублируются. Стремление объяснить целую совокупность признаков через введение более глубинных , обобщенных характеристик явления, в основном определяющих его структуру, приводит к модели факторного анализа .
Факторный анализ
• В факторном анализе предполагается, что все многообразие и структура взаимосвязей между параметрами, описывающими явление "извне" и поддающимися непосредственному измерению (признаками), обусловлены некими скрытыми, но объективно существующими причинами, так называемыми факторами , измерить которые непосредственно нельзя.
• Концепция факторного анализа, таким образом, обеспечивает "сжатие" информации, объясняя множество признаков через небольшое, как правило, число факторов.
Факторный анализ
• Факторный анализ дает основание считать его методом, позволяющим генерировать содержательные гипотезы о структуре системы признаков, о наиболее значимых, существенных признаках, о группах тесно связанных признаков.
• В основе факторного анализа лежит идея о том, что за сложными взаимосвязями измеренных признаков стоит определенная структура, отражающая наиболее существенные черты изучаемой системы, а измеренные признаки являются конкретными проявлениями скрытых общих факторов, определяющих эту структуру.
Факторный анализ
• Таким образом, поведение каждого исходного признака определяется действием на него совокупности относительно небольшого числа общих факторов , влияющих на все показатели и обусловливающих взаимосвязи между ними, и характерного фактора , воздействующего только на данный показатель.
Факторный анализ
• Каждый признак имеет собственную единицу измерения, но это означает несопоставимость его с другими признаками. В этом случае факторы, общие для целого ряда признаков разной размерности, вообще были бы лишены смысла.
• Исходя из этих соображений, в факторном анализе все величины, входящие в факторную модель, стандартизированы, т.е. являются безразмерными величинами со средним арифметическим значением 0 и средним квадратическим отклонением 1.
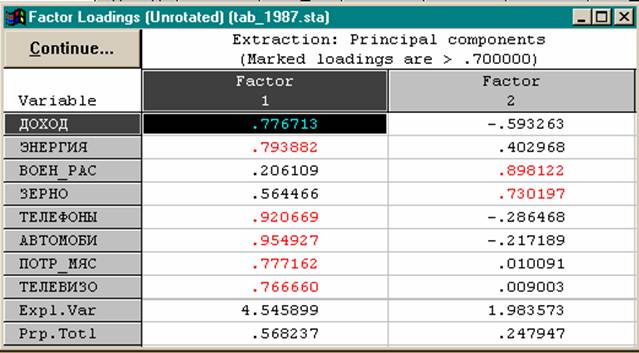
Факторные нагрузки
• Коэффициент взаимосвязи между некоторым признаком и общим фактором, выражающий меру влияния фактора на признак, называется факторной нагрузкой данного признака по данному общему фактору.
• Матрица, состоящая из факторных нагрузок и имеющая число столбцов, равное числу общих факторов, и число строк, равное числу исходных признаков, называется факторной матрицей .
Факторные нагрузки
• Основой для вычисления факторной матрицы является матрица парных коэффициентов корреляции исходных признаков.
• Как известно, корреляционная матрица фиксирует степень взаимосвязи между каждой парой признаков. Аналогично факторная матрица фиксирует степень линейной связи каждого признака с каждым общим фактором.
Факторные нагрузки
• Величина факторной нагрузки не превышает по модулю единицы, а знак ее говорит о положительной или отрицательной связи признака с фактором.
• Чем больше абсолютная величина факторной нагрузки признака по некоторому фактору, тем в большей степени этот фактор определяет данный признак.
• Значение факторной нагрузки по некоторому фактору, близкое к нулю, говорит о том, что этот фактор практически на данный признак не влияет.
Вклады факторов
• Факторная модель дает возможность вычислять вклады факторов в общую дисперсию всех признаков. Суммируя квадраты факторных нагрузок для каждого фактора по всем признакам, получаем его вклад в общую дисперсию системы признаков: чем выше доля этого вклада, тем более значимым, существенным является данный фактор.
• При этом можно выявить и оптимальное количество общих факторов, достаточно хорошо описывающих систему исходных признаков.
Вклады факторов
• Факторы выделяются последовательно, в соответствии с их вкладами в суммарную дисперсию признаков: сначала находится фактор, имеющий максимальный вклад, затем его влияние устраняется, и для матрицы остаточных корреляций снова ищется фактор с максимальным вкладом и т.д.
• Процесс последовательного нахождения факторов прекращается, если их суммарный вклад превысит определенный, заранее выбранный порог.
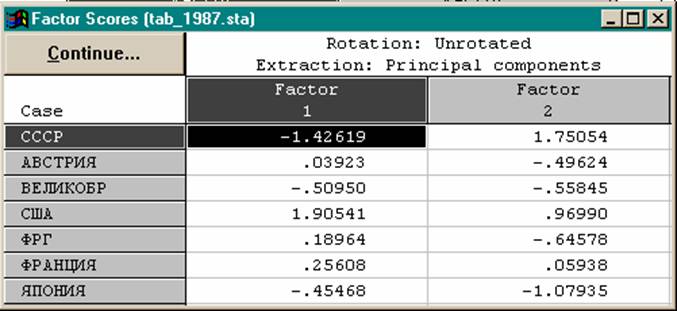
Факторные веса
• Значение (мера проявления) фактора у отдельного объекта называется факторным весом объекта по данному фактору. Факторные веса позволяют ранжировать, упорядочить объекты по каждому фактору.
• Чем больше факторный вес некоторого объекта, тем больше в нем проявляется та сторона явления или та закономерность, которая отражается данным фактором.
Факторные веса
• Факторные веса могут быть как положительными, так и отрицательными.
• В силу того, что факторы являются стандартизованными величинами со средним значением, равным нулю, факторные веса, близкие к нулю, говорят о средней степени проявления фактора, положительные – о том, что эта степень выше средней, отрицательные – о том . ч то она ниже средней.
Факторные веса
• Например, если речь идет о факторе, выражающем уровень развития в определенном аспекте, то большой факторный вес свидетельствует о высоком уровне развития данного объекта, а низкий факторный вес – о низком уровне.
Метод главных компонент
• Чрезвычайно удобным в качестве метода "сжатия" информации с целью выявления обобщенных характеристик явления является метод главных компонент – разновидность факторного анализа.
• Главные компоненты независимы, а их число равно числу исходных признаков. Обычно нескольких первых компонент оказывается достаточно для хорошего описания почти всей дисперсии исходных признаков, т.е. для описания в сжатом виде всей исходной информации
Метод главных компонент
• Практически, если число уже найденных главных компонент (или факторов) не больше, чем m /2, объясняемая ими дисперсия не менее 70%, а следующая компонента дает вклад в суммарную дисперсию не более 5%, факторная модель считается достаточно хорошей.
Работа с пакетом Statistica
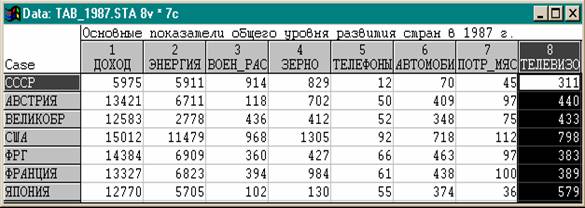
Работа с пакетом Statistica

Работа с пакетом Statistica
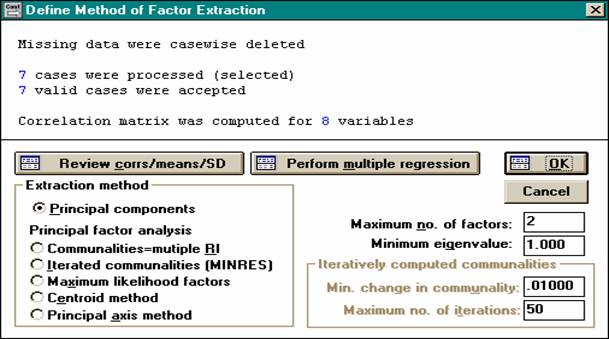
Работа с пакетом Statistica
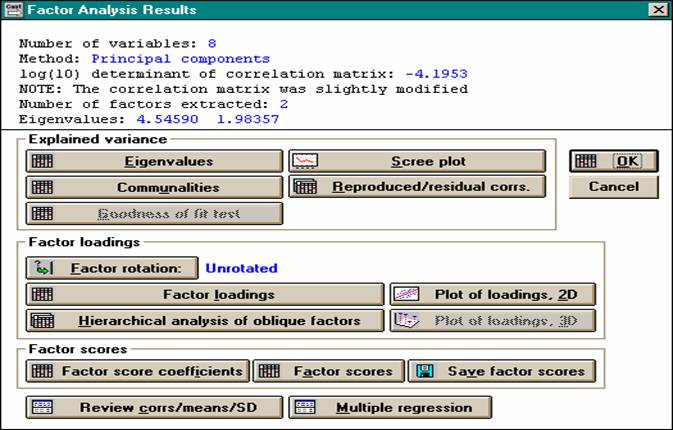
Работа с пакетом Statistica
Работа с пакетом Statistica
Факторный анализ как метод классификации
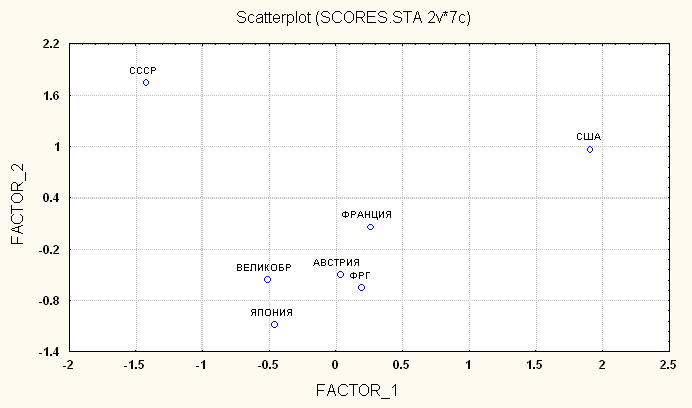
• Факторный анализ можно использовать не только как метод сжатия информации, но и как удобный подход к классификации, когда множество исходных признаков заменяется найденными обобщенными факторами.
• Идея проведения классификации объектов в пространстве немногих факторов, заменяющих большое количество исходных признаков, состоит в измерении факторов на отдельных объектах и последующей визуальной или аналитической группировке объектов на оси одного фактора или в пространстве двух факторов.
Работа с пакетом Statistica
Работа с пакетом Statistica
Работа с пакетом Statistica