АНАЛИЗ ПАРНЫХ ВЗАИМОСВЯЗЕЙ

Основные понятия

l      Статистическая связь и ее отличие от функциональной.

l      Связь как синхронность (согласованность) – корреляционный анализ.

l      Связь как зависимость (влияние) – регрессионный анализ (причинно-следственные связи).

l      Парная связь как частный случай множественной связи.

l      Неучтенные факторы.

Этапы анализа

l      Выявление наличия взаимосвязи между признаками;

l      Определение формы связи;

l      Определение силы (тесноты) и направления связи.

Выявление наличия связи между признаками

Диаграммы рассеяния

Выявление наличия связи между признаками

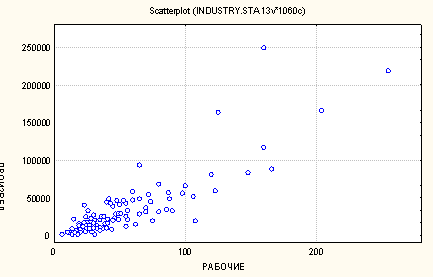
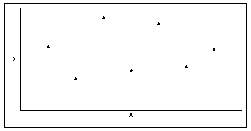
l      Простейшим визуальным способом выявить наличие взаимосвязи между количественными переменными является построение диаграммы рассеяния (scatterplot). Это график, на котором по горизонтальной оси (X) откладывается одна переменная, по вертикальной (Y) другая. Каждому объекту на диаграмме соответствует точка, координаты которой равняются значениям пары выбранных для анализа переменных.

Диаграмма рассеяния (scatterplot)

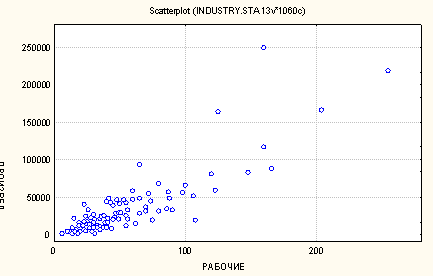
Диаграмма рассеяния

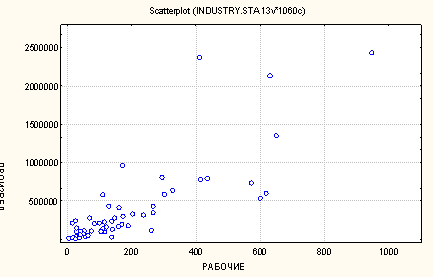
Направление связи

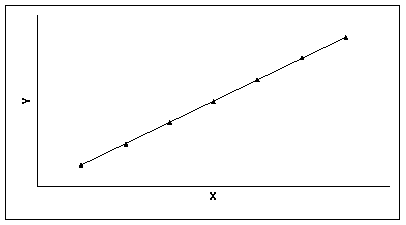
l      Если бы существовала функциональная (математически точная) положительная зависимость между числом рабочих и доходом, т.е. если бы на каждом предприятии каждый рабочий за год производил в точности одинаковое количество продукции, все точки-объекты расположились бы на «растущей» прямой.

l      В этом случае чем больше значения одного признака, тем больше значения другого ) и чем меньше значения одного признака, тем меньше значения другого.

l      Пример положительной функциональной связи между признаками X и Y.

l      Однако на практике мы встречаемся не с функциональными, а со статистическим связями (действительно, эффективность труда, т.е. количество продукции, произведенной одним рабочим, различается на разных предприятиях). Поэтому на графике точки-объекты не лежат на одной прямой, и какую бы прямую мы ни провели, все точки на нее не попадут.

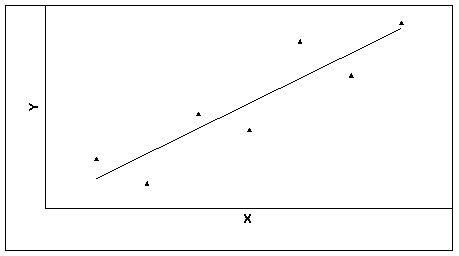
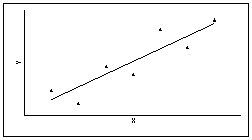
l      В случае положительной статистической связи мы видим "облако" точек, о котором можно сказать, что оно вытянуто по диагонали от левого нижнего угла к правому верхнему, т.е. с ростом одного признака другой в среднем растет.

l      Значит, и в этом случае чем больше значения одного признака, тем больше значения другого и чем меньше значения одного признака, тем меньше значения другого. Однако это верно не для каждого объекта, а для статистической совокупности.

l      Пример положительной статистической связи между признаками X и Y.

l      Если бы между признаками существовала функциональная отрицательная (а не положительная) зависимость, точки на диаграмме также расположились бы на одной прямой, однако эта прямая проходила бы в противоположном направлении.

l      В этом случае чем больше значения одного признака, тем меньше значения другого и чем меньше значения одного признака, тем больше значения другого.

l      Пример отрицательной функциональной связи между признаками X и Y.

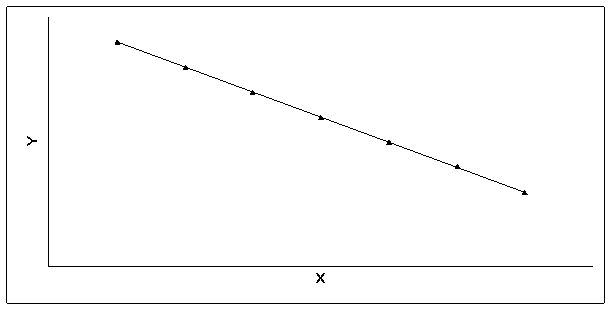
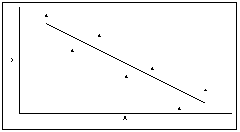
l      Для статистической отрицательной связи мы увидим на графике "облако" точек, о котором можно сказать, что оно вытянуто по диагонали от левого верхнего угла к правому нижнему, т.е. с ростом одного признака другой признак в среднем убывает.

l      Значит, и в этом случае чем больше значения одного признака, тем меньше значения другого и чем меньше значения одного признака, тем больше значения другого. Однако это верно не для каждого объекта, а для статистической совокупности.

l      Пример отрицательной статистической связи между X и Y.

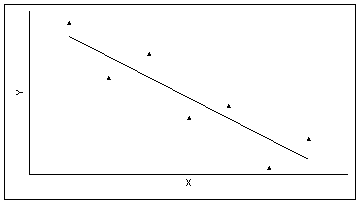
Подбор формы связи

Линейная связь

Форма связи

l      Почему прямая?

l      Если наше облако точек напоминает очертания некоторой линии, то можно предполагать, что мы видим на диаграмме рассеяния именно такую по форме зависимость, однако искаженную воздействием как случайных, так и неучтенных факторов, вызывающим отклонение точек от теоретической формы.

l      Поскольку наиболее простой формой зависимости в математике является прямая, то в корреляционном и регрессионном анализе наиболее популярны линейные модели.

l      Однако иногда расположение точек на диаграмме рассеяния показывает нелинейную зависимость либо вообще отсутствие связи между признаками.

l      Примеры нелинейной связи (рис. а) и отсутствия связи (рис. б) между признаками X и Y

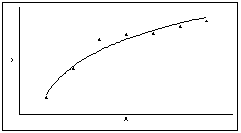
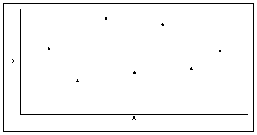
l      Попробуем провести прямую линию через облако точек на диаграмме рассеяния. Таких линий можно нарисовать множество, причем на глаз невозможно определить, какая из них лучше подходит для описания диаграммы рассеяния.

l      Однако существует метод, который позволяет совершенно точно вычислить положение прямой линии, наилучшим образом проходящей через облако точек.

l      Это – метод наименьших квадратов.

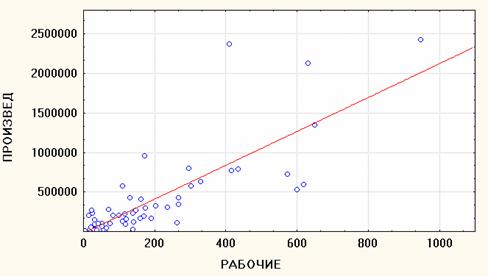
l      Вычисляемая с его помощью прямая линия называется линией регрессии. Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями).

l      Таким образом, линия регрессии дает наилучшее  приближенное описание линейной зависимости между двумя переменными.

Линия регрессии

Коэффициент корреляции

Мера тесноты линейной связи

l      Какова бы ни была конфигурация облака точек на диаграмме рассеяния – лежат ли они в точности на одной прямой, или разбросаны хаотически – любая статистическая программа всегда сможет построить уравнение регрессии. Однако в первом случае (точки лежат на одной прямой) оно будет весьма достоверным, а во втором (точки разбросаны хаотически) – нет.

l      Более того, может оказаться, что через два облака, различающихся степенью близости к линейной конфигурации, будут проведены одинаковые линии регрессии.

l      Тем не менее зависимость между двумя переменными может иметь различный характер даже при одинаковых линиях регрессии.

l      Оказывается форма связи (линия регрессии) сама по себе не дает ответа на вопрос о тесноте (силе) связи пары переменных.

l      На этот вопрос отвечает коэффициент парной корреляции. Он показывает, насколько тесно две переменные связаны между собой.

l      Визуально о силе связи можно судить по тому, насколько тесно расположены точки-объекты около линии регрессии. Чем ближе точки к линии регрессии, тем сильнее связь.

l      На каком из двух графиков связь между признаками сильнее (теснее), т.е. какому из графиков соответствует более высокий коэффициент корреляции?

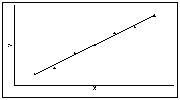
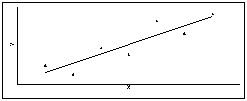
l      Коэффициент парной корреляции r принимает значения в диапазоне от –1 до +1.

l      Положительные значения коэффициента корреляции r свидетельствуют о положительной связи между признаками, отрицательные – об отрицательной связи.

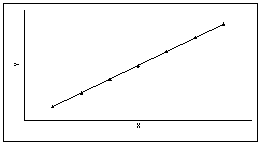
l      Если r = 1, то между двумя переменными существует функциональная положительная линейная связь, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с положительным наклоном.

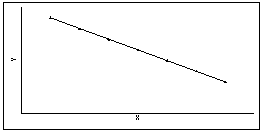
l      Если r = –1, то между двумя переменными существует функциональная отрицательная линейная зависимость, т.е. на диаграмме рассеяния соответствующие точки лежат на одной прямой с отрицательным наклоном.

l      Если r = 0, то рассматриваемые переменные линейно независимы, т.е. на диаграмме рассеяния облако точек "вытянуто по горизонтали".

l      Формула для вычисления парного коэффициента корреляции:

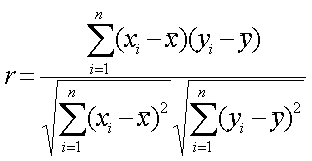
l      Коэффициент парной корреляции вычисляется для количественных признаков.

l      Коэффициент корреляции симметричен, т.е. не изменяется, если X и Y поменять местами.

l      Коэффициент корреляции является величиной безразмерной.

l      Коэффициент корреляции не изменяется при изменении единиц измерения признаков X и Y.

l      Сам по себе коэффициент корреляции не имеет содержательной интерпретации. Однако его квадрат (r2), называемый коэффициентом детерминации (обозначается d и обычно выражается в %), имеет простой смысл – это показатель того, насколько изменения зависимого признака объясняются изменениями независимого.

l      Более точно, это доля дисперсии (разброса) одного признака, объясняемая влиянием другого (если связь интерпретировать как причинно-следственную).

l      Из определения коэффициента детерминации следует, что он принимает значения в диапазоне от 0% до 100%.

l      Если две переменные функционально линейно зависимы (точки на диаграмме рассеяния лежат на одной прямой), то можно сказать, что изменение одной из них полностью объясняется изменением другой, а это как раз тот случай, когда коэффициент детерминации равен 100%  (при этом коэффициент корреляции может быть равен как 1, так и –1).

Коэффициенты корреляции и детерминации

l      Если две переменные линейно независимы (метод наименьших квадратов дает горизонтальную прямую), то одна из них в своих изменениях никоим образом не определяет другую – в этом случае коэффициент детерминации равен нулю.

l      В остальных случаях коэффициент детерминации указывает, какая часть изменений одной переменной объясняется изменениями другой переменной.

l      Чем выше по модулю (по абсолютной величине) значение коэффициента корреляции, тем сильнее связь между признаками.

l      Принято считать, что коэффициенты корреляции, которые по модулю больше 0,7, говорят о сильной связи (при этом коэффициенты детерминации > 50%, т.е. один признак определяет другой более, чем наполовину).

l      Коэффициенты корреляции, которые по модулю меньше 0,7, но больше 0,5, говорят о связи средней силы (при этом коэффициенты детерминации меньше 50%, но больше 25%).

l      Наконец, коэффициенты корреляции, которые по модулю меньше 0,5, говорят о слабой связи (при этом коэффициенты детерминации меньше 25%).

Матрица корреляции

l      Если объекты характеризуются целым набором количественных признаков, можно  построить т.н. матрицу корреляции, т.е. квадратную таблицу, число строк и столбцов которой равно числу признаков, а на пересечении каждых строки и столбца стоит коэффициент корреляции соответствующей пары признаков.

l      Матрица симметрична, т.е. значения выше и ниже диагонали повторяются (т.к. rxy = ryx).

l      Пример матрицы корреляции для трех признаков. В этой матрице 9 коэффициентов: по диагонали 3 единицы (корреляция каждого признака с самим собой) и три коэффициента для трех пар признаков: r12, r13 и r23, которые повторяются выше и ниже диагонали.

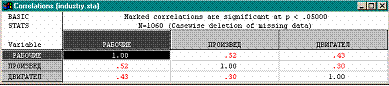
l      Некоторые коэффициенты в матрице корреляции показаны красным цветом.

l      Это означает, что они являются статистически значимыми.

l      В чем смысл понятия статистической значимости применительно к коэффициенту корреляции?

Значимость коэффициента корреляции

Статистическая значимость коэффициента корреляции

l      Если коэффициент корреляции вычислен на основе выборочных данных, то не исключено, что его ненулевое значение является не отражением действительной связи между признаками, а просто получено в результате специфики данной выборки (тогда как в генеральной совокупности коэффициент корреляции равен нулю, т.е. линейной связи между признаками нет).

l      Таким образом, надо понять, как далеко значение r от нуля.

l      Если значение коэффициента корреляции вычислено по выборочным данным, то для оценки его значения в генеральной совокупности, как обычно, строится доверительный интервал.

l      Для построения доверительного интервала вычисляется ошибка коэффициента корреляции sr по формуле:

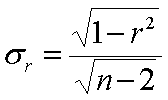
l      Затем ошибка коэффициента корреляции умножается на параметр t, зависящий от доверительной вероятности P ( для вероятности 95% t = 2), чтобы найти предельную ошибку.

l      Наконец, строится доверительный интервал r ± σr и проводится проверка, попадет ли нулевое значение в этот интервал.

l      Если ноль не попадет в доверительный интервал, значит с высокой вероятностью в генеральной совокупности не может быть нулевого значения коэффициента корреляции, т.е. связь между признаками существует и в генеральной совокупности. В таком случае коэффициент корреляции является статистически значимым.

l      -1                                            0                         r                   1

l       

l      Если ноль попадет в доверительный интервал, значит с высокой вероятностью в генеральной совокупности может оказаться нулевая корреляция, т.е. отсутствие связи. В таком случае коэффициент корреляции является статистически незначимым.

l      -1                                            0                   r                        1

l      Значимые коэффициенты в программе Statistica показаны красным цветом, незначимые – черным. Незначимые коэффициенты можно считать нулями и принимать во внимание только значимые.

l       

l      Необходимо подчеркнуть, что величина коэффициента корреляции еще не гарантирует его значимости: даже большой коэффициент может оказаться статистически незначимым (например, при малом объеме выборки), а небольшой коэффициент (если выборка велика) - значимым.