[Материалы для студентов-историков]
Информатика и математика - материалы для экзамена
МНОГОМЕРНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Введение
l Как показывает опыт анализа массовых источников, число объектов может достигать многих десятков и сотен; число признаков также может исчисляться десятками. Очевидно, непосредственный (визуальный) анализ матрицы данных при большом количестве объектов и признаков практически малоэффективен – можно лишь выявить отдельные особенности изучаемой структуры, извлечь иллюстративные, частные примеры.
l При этом возникают задачи укрупнения, концентрации исходных данных, т.е. построения обобщенных характеристик множества признаков и множества объектов. Решение этих задач может осуществляться с помощью современных методов многомерного статистического анализа.
l Методы, ориентированные на анализ структуры множества признаков и выявление обобщенных факторов, известны как методы факторного анализа, а методы анализа структуры множества объектов образуют совокупность методов многомерной классификации.
l Методы многомерной классификации позволяют группировать объекты с учетом всех существенных структурно-типологических признаков и характера распределения объектов в заданной системе признаков.
l Такая классификация производится на основе стремления собрать в одну группу в некотором смысле схожие объекты, причем так, чтобы объекты из разных групп были по возможности несхожими.
Кластер-анализ
l Пусть все m признаков являются количественными. Тогда каждый из n объектов может быть представлен точкой в m-мерном пространстве признаков.
l Характер распределения этих точек в пространстве признаков определяет структуру сходства и различия объектов в заданной системе показателей. О сходстве объектов можно судить по расстоянию между соответствующими точками.
l Содержательный смысл такого понятия сходства означает, что объекты тем более близки, похожи, чем меньше различий между значениями одноименных показателей.
l Для определения близости пары точек (объектов i и j) в многомерном пространстве количественных признаков используется евклидово расстояние, равное корню квадратному из суммы квадратов разностей значений одноименных показателей, взятых для данной пары объектов.
l Расстояние между объектами зависит от "масштаба" признаков: признаки, диапазон значений которых велик, играют большую роль при вычислении расстояния между объектами в отличие от признаков, диапазон изменения которых мал. Например, расстояния, выраженные в километрах, будут в тысячу раз меньше, чем в метрах.
l По этой причине данные обычно нормализуют, т.е. все признаки приводят к стандартному виду со средним значением, равным нулю, и стандартным отклонением, равным единице.
l После нормализации объекты на оси каждого признака сохраняют свое относительное положение, но "масштаб" измерения признаков становится единым.
l Если подсчитать расстояния для всех пар объектов, получится квадратная таблица D размером m ´ m (матрицу расстояний); матрица расстояний, очевидно, симметрична, поскольку расстояние от объекта i до объекта j в точности такое же, как и расстояние от объекта j до объекта i.
Агломеративно-иерархический метод
l Матрица расстояний D служит основой агломеративно-иерархического метода, основная идея которого заключается в последовательном объединении группируемых объектов – сначала самых близких, а затем все более удаленных друг от друга.
l Процедура построения классификации состоит из последовательных шагов, на каждом из которых производится объединение двух ближайших групп объектов (кластеров). Кластер (от англ. Cluster) - скопление, “гроздь”, группа объектов, характеризующихся общими свойствами.
l Существуют различные способы определения расстояний между кластерами (различающие методы кластерного анализа). Обычно близость двух кластеров определяется как среднее значение расстояния между всеми такими парами объектов, где один объект пары принадлежит к одному кластеру, а другой – к другому.
l На первом шаге процедуры агломеративно-иерархического метода определяется пара объектов, расстояние между которыми минимально.
l Эти объекты объединяются в один кластер, в матрице вычеркиваются строка и столбец, соответствующие первому из этих объектов, а расстояния от нового кластера до всех остальных кластеров (объектов) вычисляются как средние из расстояний от объектов первого кластера до всех остальных.
l И наконец, эти значения заносятся в строку и столбец матрицы расстояний, соответствующие второму объекту из первого кластера.
l На втором шаге процедуры по матрице расстояний, уменьшенной на одну строку и один столбец, снова определяют минимальное расстояние и формируют новый кластер. Этот кластер может быть построен в результате объединения либо двух объектов, либо одного объекта с кластером, построенным на первом шаге.
l Снова в матрице расстояний вычеркиваются одна строка и один столбец, а одна строка и один столбец пересчитываются и т.д.
l Таким образом, иерархический метод кластерного анализа включает n – 1 аналогичных шагов.
l При этом после выполнения каждого шага число кластеров уменьшается на единицу, а матрица расстояний уменьшается на одну строку и один столбец. В конце этой процедуры получится один кластер, объединяющий все n объектов.
l Результаты такой классификации часто изображают в виде дендрограммы (дерева иерархической структуры), содержащего n уровней, каждый из которых соответствует одному из шагов описанного процесса последовательного укрупнения кластеров.
Пример
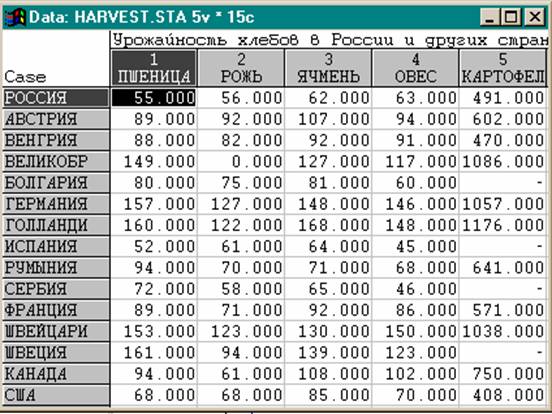
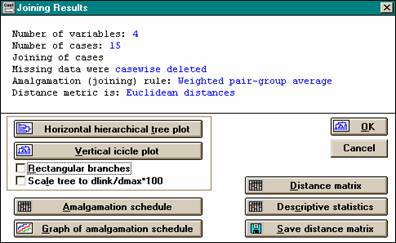
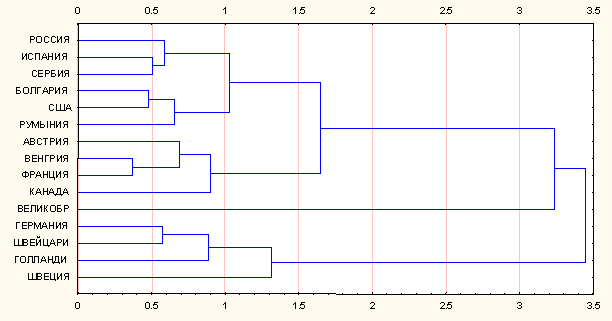
Пример
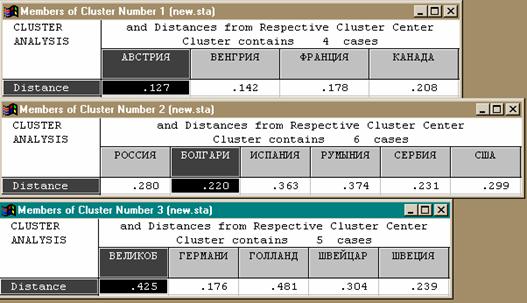
l Анализируя структуру полученной классификации, можно видеть, что страны могут быть разделены на три группы (Германия, Швейцария, Голландия и Швеция); (Австрия, Венгрия, Франция и Канада); (Россия, Испания, Сербия, Болгария, США, Румыния).
l При этом третья группа состоит из двух подгрупп: Россия, Испания и Сербия входят в одну из них, а Болгария, США и Румыния – в другую.
l Кроме того, вторая и третья группы на определенном уровне образуют общий кластер, тогда как первая группа остается достаточно далекой от этого кластера.
l Возникает вопрос: почему Великобритания не вошла ни в один из трех кластеров, но занимает особое положение на схеме? Если внимательно посмотреть на исходные данные, то причина станет ясна: в соответствующем столбце исходной таблицы стоит нулевое значение.
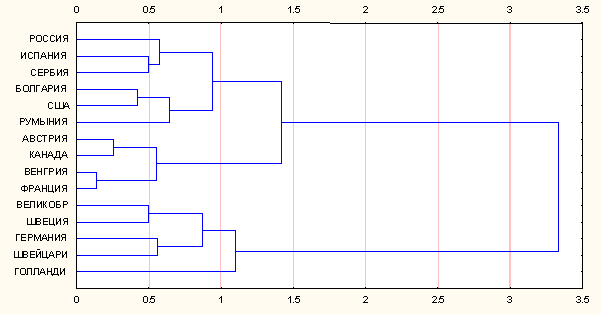
l Скорректируем параметры классификации, исключив из признаков, по которым проводится анализ, переменную "рожь".
l Затем повторим процедуру классификации и рассмотрим новый результат.
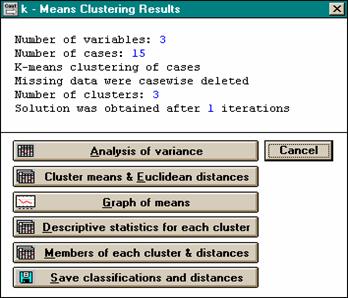
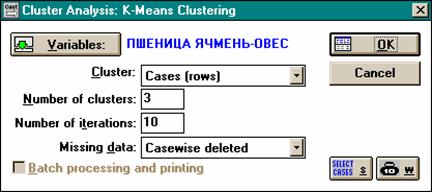
Метод k-средних
l Другим методом кластерного анализа является т.н. метод k-средних. В отличие от агломеративно-иерархического метода, который не требует предварительной оценки возможного числа групп объектов, этот метод основан на гипотезе о наиболее вероятном количестве классов. Задачей метода при этом является построение заданного числа кластеров, которые должны максимально отличаться друг от друга.
l Процедура построения кластеров начинается со случайной группировки объектов. Затем следует итерационный процесс перемещения объектов между группами с целью минимизировать внутриклассовую дисперсию показателей и максимизировать межклассовую дисперсию (т.е. каждый кластер должен состоять из максимально "похожих" объектов, а сами кластеры должны быть максимально "непохожими" друг на друга).
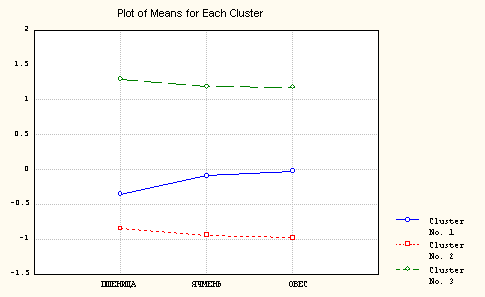
l Результаты этого метода позволяют получить центры всех классов (и другие параметры дескриптивной статистики) по каждому из исходных признаков, а также увидеть графическое представление о том, насколько и по каким параметрам различаются полученные классы.
Пример
Нечеткая классификация
l Сложность, неоднородность систем, изучаемых исторической наукой, проявляется и в том, что объекты принадлежащие к одному типу, в разной мере обладают присущими ему свойствами. Следовательно, при выделении типов (классов) объектов следует учитывать наличие ядра класса и его периферии.
l Ядро типа представляет такую группу объектов, для которых характерно концентрированное выражение всех специфических свойств типа, определяющих качественное отличие данного типа от всех иных.
l Нечеткое множество – это класс объектов, в котором нет резкой границы между теми объектами, которые входят в этот класс, и теми, которые в него не входят.
l Принадлежность каждого объекта к нечеткому множеству описывается с помощью величины, принимающей значения от 0 до 1. Эта величина называется степенью принадлежности; чем ближе она к 1, тем больше степень принадлежности объекта к данному нечеткому множеству.
l При использовании ТНМ (теории нечетких множеств) неопределенность связана с размытостью границ между классами.
l Понятие нечеткости относится к классам, в которых могут иметься различные степени принадлежности, промежуточные между полной принадлежностью (1) и непринадлежностью (0) объектов к классу. В этом случае неопределенность не связана со случайностью, она сохраняется и при наличии полной информации об объектах.
l Ядро нечеткого множества определяется как такой набор объектов, для каждого из которых степень принадлежности к данному нечеткому множеству превышает некоторое пороговое значение (например, 0,9).
Пример
Нечеткая классификация
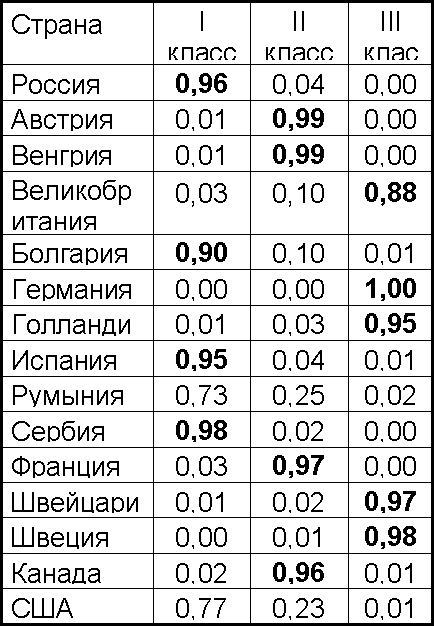
l Приведенные результаты в целом соответствуют полученным ранее. Выделим ядро каждого класса по порогу принадлежности, равному 0,8.
l В первый класс вошли Россия, Болгария, Испания, Румыния, Сербия и США. Однако в отличие от результатов "жесткой" классификации видно, что только четыре из этих шести стран входят в ядро класса, тогда как Румыния и США относятся к его периферии, обнаруживая некоторое сходство с объектами второго класса.
l В определенной степени эти страны являются объектами, переходными от первого ко второму классу.
l Во второй класс вошли, как и раньше, Австрия, Венгрия, Франция и Канада, причем все они относятся к ядру этого класса.
l То есть, второй класс является более "сплоченным", чем первый (то же самое можно сказать и о третьем классе). На рис. 6.14 видно, что в целом 11 стран из 15 входят в свои классы с весом принадлежности от 0,9 до 1, две страны входят с весом от 0,8 до 0,9 и две – с весом от 0,7 до 0,8 (Румыния и США).